티스토리 뷰
위상정렬
위상정렬 은 부분 순서를 갖는 집합을 정렬하는 방법입니다. 우리에게 익숙한 순서가 부여되는 집합인 전순서 집합에는 자연수, 실수 등이 있습니다. 이들은 임의의 원소를 두 개 꺼내면 둘 사이의 순서를 언제나 결정할 수 있는 게 특징입니다. 이와 다르게 모든 임의의 두 원소 사이에 순서를 결정하지 못하는 집합도 있습니다. 하지만 뭔가 집합에 포함된 순서가 있으면서도 말이죠. 알쏭달쏭 하지만 그런 문제는 일상에 많습니다.
흔히 드는 예시는 수강신청입니다. 수강하려는 과목들 사이에는 딱히 순서가 없지만, 어떤 과목에는 선수과목이 있곤 합니다. 이런 경우 부분적으로 발생하는 순서를 고려해서 수강 계획을 짜야하죠. 이처럼 작업관리에서는 흔하게 부분 순서를 갖는 문제를 쉽게 마주합니다. 이를 정렬할 수 있는 방법 중 하나가 위상정렬입니다.
위상정렬의 결과
위상정렬로 정렬한 결과는 한 가지가 아닙니다. 위상 순서를 만족하는 결과는 여러 모습일 수 있습니다. 다음 예시를 보겠습니다.

이런 유향 그래프를 정렬하는 결과는 다음과 같이 여러 가능성 모두 만족합니다.
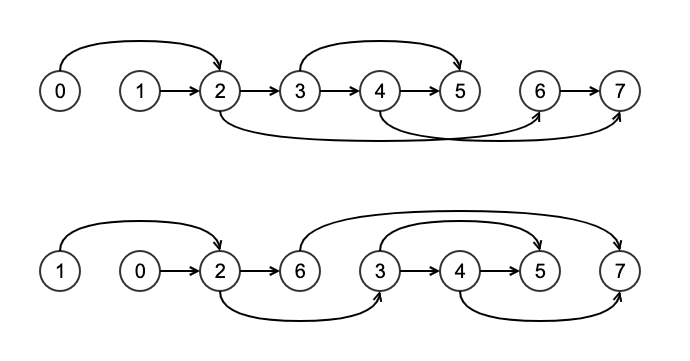
필요에 의해 이 중 하나를 사용해도 부분 순서를 충분히 만족하는 정렬 결과를 기대할 수 있습니다. 부분 순서란 전체 순서와 달리 모든 원소 간의 순서가 결정되지 않기 때문에 생기는 특성입니다. 이 특성을 이용해 약간 다른 형태의 결과를 만들 수도 있습니다.
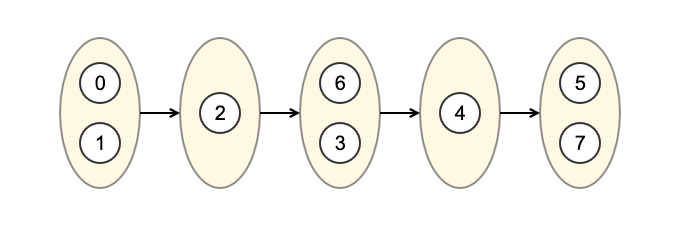
중간에 어떠한 규칙에 의해 그룹을 만들었습니다. 일단 이 결과에 위 초기 그래프에서 나타난 부분 순서를 모두 적용해보면 충분히 만족한다는 점을 확인할 수 있습니다. 0과 1 사이에는 순서가 없으며 4는 5보다 먼저 오고, 6은 여전히 7보다 앞서 있습니다. 일반적인 위상정렬은 부분 순서를 만족하는 한 줄로 세우곤 합니다. 하지만 사실 꼭 그럴 필요는 없습니다. 이렇게 그룹 지어진 결과가 주는 해석을 활용한 상황이 있을 수 있습니다. 사례는 뒤에서 적도록 하고 먼저 이 결과를 만드는 방법입니다.
아주 간단하고 위상정렬의 알고리즘을 변형하는 것도 아닙니다. 단지 노드를 하나씩 찾는 것이 아니라 한 번의 순회 검사에서 가능한 모든 "참조가 0"인 정점을 확인하는 것입니다.

이 결과에서 같은 그룹에 속한 노드들은 다음과 같은 작은 사실을 만족합니다.
- 서로 간에 순서가 없다
- 서로 간에 의존도 없다
사실 두 문장은 같은 의미지만 순서도 의존도 없는 관계의 것들이라면 어떤 활용이 가능할까요? 바로 동시에 처리해도 안전한 작업들이라는 점입니다.
그룹핑 위상정렬
이와 같은 정렬의 구현을 간단히 살펴봅시다. 먼저 그래프를 표현할 Edge 는 다음과 같습니다. 도착점을 기준으로 시작점을 모아두는 편이 좋습니다.
data class Edge<T> constructor(val from: Set<T>, val to: T)그리고 정렬은 다음과 같습니다.
fun <T> sort(edges: Collection<Edge<T>>): List<Set<T>> {
if (edges.isEmpty()) { // 종료 조건
return listOf()
}
val initials = edges.filter { it.from.isEmpty() }.toSet() // 피참조가 0인 node 목록
val head = listOf(initials.map { it.to }.toSet()) // 새 그룹
return head + sort(clearInitials(edges, initials)) // 재귀
}현재 시점에 피참조가 0 인 node 들을 모두 찾습니다. 이들을 그룹지어 결과에 순서대로 포함합니다. 매우 쉽게 정렬과 그룹핑을 구현할 수 있습니다. 그리고 남은 그래프에서 그룹에 포함한 node 는 빼고 다시 진행하면 됩니다. 이 node 들을 빼는 것은 중요한 코드는 아니지만 아래에 간단히 첨부합니다.
private fun <T> clearInitials(edges: Collection<Edge<T>>, initials: Set<Edge<T>>): Collection<Edge<T>> {
val nodes = initials.map { it.to }
return (edges - initials) // initial node 제거
.map { Edge(it.from - nodes, it.to) } // initial node 로 부터의 edge 제거
}이제 예제 그래프를 넣어 정렬 결과를 확인해봅니다.
fun main() {
val sorted = sort(
listOf(
Edge(setOf(), 0),
Edge(setOf(), 1),
Edge(setOf(0, 1), 2),
Edge(setOf(2), 3),
Edge(setOf(3), 4),
Edge(setOf(3, 4), 5),
Edge(setOf(2), 6),
Edge(setOf(4, 6), 7)
)
)
println(sorted)
}위 예시와 같은 결과를 확인할 수 있습니다.
[[0, 1], [2], [3, 6], [4], [5, 7]]안전한 최소한의 동시성
만약 일련의 작업들을 수행해야 하는 과정에서 부분적인 순서(또는 의존관계)가 있는 무거운 작업들을 다뤄야 한다면 우리는 동시적으로 다룰 수 있는 부분들에 대해 관심을 가질 수 있습니다. 하지만 동시에 진행해도 괜찮은 부분들을 찾는 과정에 부분적인 순서를 고려해서 설계하는 것은 조금 까다로운 일입니다. 만약 그 작업이 100개가 넘게 주어진다면 실상 일일이 설계하여 동시성을 확보하는 건 어려운 일입니다.
사실 이럴 때 사용하는 도구가 바로 위상정렬이니 이 문제를 위해 위상정렬을 도입하는 것은 흔한 해결책입니다. 이점에서 위상정렬이 가지고 있는 그룹핑을 더한다면 우리는 증명된 매우 안전한 동시성 설계를 하나 확인할 수 있게 되는 것입니다. 위상정렬의 결과로 얻어낸 동시성 설계는 매우 엄밀하지는 않습니다. 이른바 최대의 동시성을 확보하는 것은 아닙니다. 노력한다면 더 좋은 동시성 설계를 만들 수도 있습니다. 하지만 위상정렬로 얻은 결과는 최소한의 동시성 설계 역할은 충분히 할 수 있습니다. 알고리즘에 의해 자동화할 수 있는 안전하게 증명된 최소한의 동시성 설계인 것입니다.
만약 작업의 추가, 변경 등이 잦은 도메인이라면 더욱더 이러한 자동화된 동시성 설계가 힘을 발휘할 것입니다. 실제로 진행하는 프로젝트에 위와 같은 필요가 있었습니다. 작업의 양은 총 121개였고 각자 의존관계에 따른 순서를 보장받아야 하는 상황이었습니다.
스프링을 기반한 프로젝트였기에 각 작업을 진행해야 하는 부분에 @DataBean 이라는 어노테이션으로 의존과 작업의 결과를 확인하도록 하였습니다.
@DataBean
public SomeResult process(TaskResult tr, AnotherTaskResult atr) { /* ... */ }이 @DataBean 이 마킹된 메서드로부터 자신의 역할과 의존을 확인할 수 있습니다. 이 메서드의 입력 파라미터는 다른 작업의 결과로 주입받아야 할 의존관계를 나타내고, 메서드의 결과는 다른 작업에 필요한 데이터를 Context에 제공할 수 있음을 나타냅니다. 이렇게 형성된 의존관계 그래프를 통해 위상정렬을 통한 동시성 설계를 진행하였고, 121개의 작업은 최대 28개의 동시에 진행 가능한 작업을 확보한 총 13개의 스텝으로 분석되었습니다. 이제 121개의 작업은 총 13번의 인과적 처리과정만 거치면 모두 수행 가능한 것입니다. 이 분석은 매번 작업 사항에 변경이 발생하더라도 자동으로 분석이 진행됩니다.
정리
다시 말하지만 이 해석은 위상정렬 그 이상도 이하도 아닙니다. 위상정렬은 특성상 정렬의 결과가 여러 형태일 수 있고, 그 중에 그룹을 지을 수 있는 형태로 결과를 해석할 수도 있다는 것뿐입니다. 그 그룹에 포함된 원소 간에는 순서가 없다는 아주 작고 당연한 특성을 하나 가지고 있고 그 특성은 동시성 설계에서 매우 적절한 특성이 된다는 점이죠. 이를 이용하여 안전하게 증명 가능한 최소한의 동시성 설계를 만들어낼 수 있다는 점은 그 간단함에 비해 꽤 좋은 실용이었습니다. 이 방법에 대해서 제 경험을 소개하는 것과 함께 익숙한 문제 해결 방법으로부터 실용적인 해법을 찾은 사례로 기록해봅니다.
긴 글 읽어주셔서 감사합니다.
'Infra' 카테고리의 다른 글
| 짧고 굵게 지마켓 API Gateway 사용하기 (0) | 2022.09.14 |
|---|---|
| 가볍게 시작하는 Databricks Community Edition 환경설정 for Spark (1) | 2022.09.07 |
| MySQL만 써봤는데... MongoDB 프로젝트에 투입됐다🤯 (3) | 2022.08.05 |
| 확장성 높은 카프카 구성을 위한 서비스 설계 (0) | 2022.07.29 |
| Multi Data Source 에서 Data 모으기 (0) | 2021.06.09 |
