티스토리 뷰
안녕하세요. Club & Discount Engineering 팀에서 지마켓 할인/쿠폰 개발 업무를 맡고 있는 윤영택입니다. 저희 팀은 할인/쿠폰/수수료 등 돈과 관련된 도메인을 다루다 보니 코드를 작성할 때 BigDecimal 타입을 굉장히 많이 쓰고 있습니다. 본 포스팅을 통해 BigDecimal을 사용해야 하는 이유와 개념, 그리고 사용법을 간단하게 소개해보고자 합니다.
1. 서론
float와 double의 문제점
여러분은 혹시 소수(decimal)를 다룰 때 다음과 같은 경험이 있으신가요?
아래 코드를 보면 특정 조건에 맞춰 함수가 실행되는 것을 기대했는데, 실제론 실행되지 않습니다.
결괏값을 출력해보면 기대와 다른 값이 나오는 것을 확인할 수 있습니다.
double a = 0.1;
double b = 0.2;
// expect true
if (a + b == 0.3) {
doSomething(); // but not invoked..
}
System.out.println(a + b); // 0.30000000000000004비슷하게 float와 double의 문제를 단적으로 보여주는 코드를 하나 더 보겠습니다. 분명 똑같은 값을 더하고 뺐는데 완전히 엉뚱한 값이 나왔습니다.
// https://gist.github.com/typestruct/0de28a74f49db5eaead8
public class Java_float_double_RoundingError {
public static void main (String[] args) {
//add (3) identical floats then subtract (3) identical floats (should be 0)
System.out.println ( .1f + .1f + .1f - .1f - .1f - .1f ); //output : 1.4901161E-8
//add (3) identical doubles then subtract (3) identical doubles (should be 0)
System.out.println ( .1d + .1d + .1d - .1d - .1d - .1d ); //output : 2.7755575615628914E-17
}
}앞선 예시들은 float와 double이 정확한 값(precise value)이 아닌 근삿값(approximate value)을 담고 있어서 발생하는, 부동소수 타입의 대표적인 문제라고 할 수 있습니다. 문제의 원인을 파악하기 위해선 고정소수점과 부동소수점에 대한 이해가 필요합니다.
고정소수점과 부동소수점
컴퓨터 세계엔 실수를 표현하는 방식엔 크게 두 가지가 있습니다. 바로 고정소수점 표현방식과 부동소수점 표현방식입니다.
1) 고정소수점 표현방식(fixed point number representation)
고정소수점 표현방식은 실수를 부호 비트(signed bit), 정수부(integer part)와 소수부(fractional part)로 나누고, 자릿수를 고정하여 실수를 표현하는 방식입니다. 예를 들어 7.75라는 실수를 2진수로 변환하면 111.11이 되는데, 이를 각각 지수부와 소수부에 담아 표현합니다. (그림은 32비트 기준)
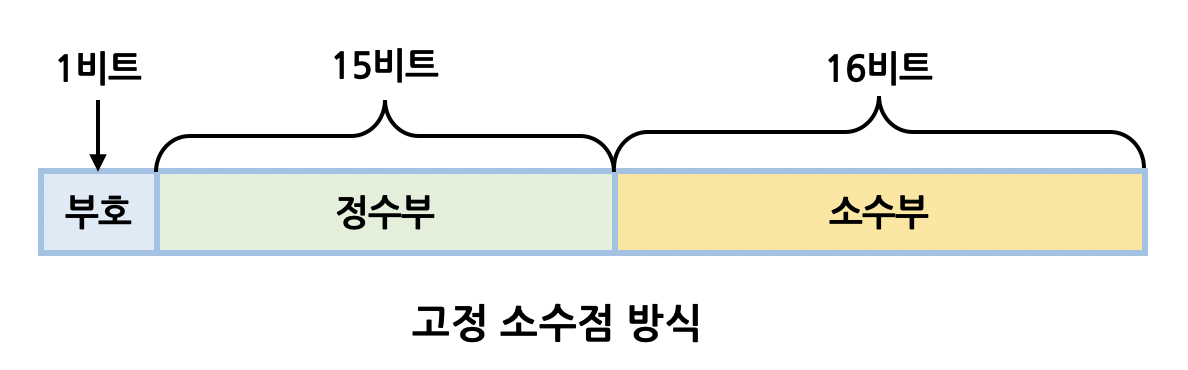

고정소수점 표현방식은 구현하는 방법이 간단하다는 장점이 있지만, 자릿수가 제한되어 있으므로 표현할 수 있는 수의 범위가 한정적이라는 치명적인 단점이 있습니다. 이에 따라 더 넓은 범위의 실수를 표현하기 위해 부동소수점이라는 개념이 등장했습니다.

2) 부동소수점 표현방식(floating point number representation)
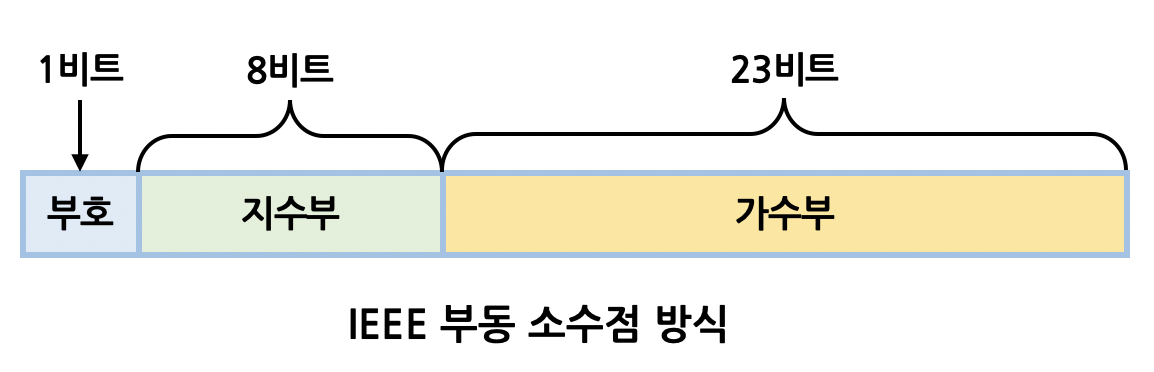

부동소수점 표현방식은 실수를 부호부(sign), 가수부(mantissa), 지수부(exponent)로 나누고, 정규화된(normalized) 값을 각 비트에 나눠 담아 실수를 표현하는 방식입니다. 쉽게 생각해서 12.3456를 저장한다면 표현식을 0.123456 * 10^2로 변경한 다음, 가수부에는 0.123456을 담고 지수부에는 2를 저장하는 방식입니다. 이해를 돕기 위해 간단하게 말씀드렸지만 실제로는 IEEE 754 표준에 따라서 지수부에 bias라는 값을 더해주는 과정을 거치게 됩니다.
부동소수점 표현방식은 고정소수점 표현방식에 비해 표현범위가 더 넓지만, 근본적으로 2진수를 사용하므로 여전히 소수를 표현할 때 오차가 발생하게 됩니다. 예컨대 0.3을 2진수로 변환하면 0.0100110011...처럼 특정 수가 무한적으로 반복됩니다. float와 double이 이와 같은 부동소수점 표현방식으로 구현되었기 때문에 앞선 문제들이 발생했던 것입니다.
고정소수점과 부동소수점에 관한 보다 자세한 내용은 여기를 참고해주세요.
2. 본격적으로 BigDecimal 살펴보기
BigDecimal이란?
공식문서에선 BigDecimal을 불변의 성질을 띠며, 임의 정밀도와 부호를 지니는 10진수라고 표현합니다. 임의 정밀도(arbitrary-precision)란 용어가 조금 낯설 수 있는데, 쉽게 말하자면 아무리 큰 숫자라도 표현할 수 있는 것을 의미합니다(실제론 무한에 가까울 뿐 무한은 아닙니다). 임의 정밀도 연산은 플랫폼마다 구현에 차이는 있지만 기본적으로 큰 숫자를 배열에 나눠 담는 방식으로 구현됩니다.
큰 숫자 = [int] + [int] + [int] + [int] + ...임의 정밀도에 관한 보다 자세한 내용은 여기를 참고해주세요.
BigDecimal은 내부적으로 임의 정밀도 연산을 활용하는 동시에 불변이므로 BigDecimal 객체 간의 연산마다 새로운 객체를 생성합니다. 이에 따라 float나 double과 같은 기본 타입에 비해 사용하기가 훨씬 느리며, 사용방법도 어렵습니다. 물론 int나 long이라는 대체제가 있지만, 실수를 표현할 수 없고 값의 범위가 비교적 제한된다는 점 때문에 BigDecimal은 금융 관련 계산에서 필수적으로 사용됩니다.
BigDecimal의 구성과 생성
BigDecimal은 개념적으로 임의 정밀도 정수형인 unscaled value와 소수점 오른쪽의 자릿수를 나타내는 32비트 정수인 scale로 구성됩니다. 예를 들어 BigDecimal 3.14의 경우 unscaled value는 314이고 scale은 2가 됩니다.
내부적으로 살펴보면 `intVal`, `scale`, `percision`, `intCompact`로 구성되어 있습니다. intVal은 BigInteger 타입으로서 unscaled value를 저장하는 변수입니다. scale은 소수점 오른쪽의 자릿수, percision은 총 자릿수를 나타냅니다. 특이한 점은 intCompact가 long 타입으로 선언되어 있다는 것인데, 만약 값의 크기가 작아서 유효숫자의 절댓값이 long 타입으로 표현될 수 있다면 BigDecimal은 unscaled value를 intVal 대신 intCompact에 저장함으로써 메모리를 최적화합니다.
package java.math;
public class BigDecimal extends Number implements Comparable<BigDecimal> {
private final BigInteger intVal; // = unscaled value
private final int scale;
private transient int precision;
private final transient long intCompact;
...
다음으로는 BigDecimal의 생성 방법에 대해 알아보겠습니다. BigInteger, char[], double, int, long, String 등 다양한 타입을 통해 BigDecimal을 생성할 수 있습니다.
BigDecimal fromBigInteger = new BigDecimal(new BigInteger("1000"));
BigDecimal fromCharArray = new BigDecimal(new char[]{'1', '5', '4', '3'});
BigDecimal fromInt = new BigDecimal(1000);
BigDecimal fromLong = new BigDecimal(10000000L);
BigDecimal fromDouble = new BigDecimal(1.12); // 이렇게 사용하면 안 됨!
이때 주의할 점은 double을 통해서 BigDecimal을 생성하면 안 된다는 것입니다. 앞서 언급했듯이 double은 근삿값을 담고 있기 때문에 BigDecimal에 이 근삿값이 고스란히 담기게 됩니다. 실제로 출력해보면 엉뚱한 값이 나오는 것을 확인할 수 있습니다.
BigDecimal fromDouble = new BigDecimal(1.12);
System.out.println(fromDouble); // 1.12000000000000010658141036401502788066864013671875대신 String 생성자나 valueOf() 정적 팩터리 메서드를 사용해서 BigDecimal을 생성해야 합니다. valueOf() 메서드는 double을 String으로 변환한 후 BigDecimal을 생성합니다.
new BigDecimal("1.12"); // 1.12
BigDecimal.valueOf(1.12); // 1.12
BigDecimal 연산
다음으로는 본격적으로 BigDecimal의 연산에 대해서 알아보겠습니다. Java에서 BigDecimal을 연산하는 방법은 기본 타입에 비해서 다소 복잡한 반면, 연산자 오버로딩을 지원하는 Kotlin에서는 BigDecimal을 연산하는 방법이 좀 더 간편합니다.
1) 사칙연산
주목할 부분은 나눗셈입니다. 기본적으로 BigDecimal은 소수점 처리(rounding)을 하지 않고 정확한 몫을 반환합니다. 만약 1 나누기 3처럼 몫의 값이 무한소수인 경우(Non-terminating decimal expansion)엔 ArithmeticException이 발생합니다. 따라서 나누기 연산을 수행할 땐 반드시 소수점 처리 전략을 지정해줘야 합니다. 소수점 처리에 대해서는 아래에서 별도로 설명하도록 하겠습니다.
Java
BigDecimal a = new BigDecimal("7");
BigDecimal b = new BigDecimal("3");
// 더하기
// 10
a.add(b);
// 빼기
// 4
a.subtract(b);
// 곱하기
// 21
a.multiply(b);
// 나누기 - 기본적으로 정확한 몫을 반환함
// 2.33333...
// java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
a.divide(b);
// 나누기 - 소수점 아래 첫째 자리까지 반올림
// 2.3
a.divide(b, 1, RoundingMode.HALF_UP);
// 나누기 - 총 자릿수를 34개로 제한하고 반올림(HALF_EVEN)
// 2.333333333333333333333333333333333
a.divide(b, MathContext.DECIMAL128);
// 나누기 - 총 자릿수를 제한하지 않고 반올림
// 2.33333...
// java.lang.ArithmeticException: Non-terminating decimal expansion; no exact
a.divide(b, MathContext.UNLIMITED);
// 나머지(%)
// 1
a.remainder(b);
// 나머지(%) - 총 자릿수를 34개로 제한
// 1
a.remainder(b, MathContext.DECIMAL128);
// 절대값
// 3
new BigDecimal("-3").abs();
// 최대값
// 7
a.max(b);
// 최소값
// 3
a.min(b);
// 부호 변환
// -7
a.negate();Kotlin
val a = BigDecimal("7")
val b = BigDecimal("3")
// a.add(b)와 동일
// 10
a + b
// a.subtract(b)와 동일
// 4
a - b
// a.multiply(b)와 동일
// 21
a * b
// a.divide(b, RoundingMode.HALF_EVEN)와 동일
// 2
a / b
// Java와 동일한 방법으로 메서드를 호출할 수도 있다
// 2.3
a.divide(b, 1, RoundingMode.HALF_UP)
2) 비교연산
equals()는 unscaled value와 scale을 모두 비교하고, compareTo()는 unscaled value만을 비교합니다. 따라서 소수점 맨 끝의 0을 무시하고 값만을 비교하고 싶다면 compareTo()를 사용해야 합니다. Kotlin에서는 사칙연산과 마찬가지로 연산자 오버로딩이 적용됐지만, == 비교의 경우 equals()가 호출되므로 이에 주의해야 합니다. 부등식에서는 compareTo()가 호출됩니다.
Java
BigDecimal a = new BigDecimal("3.14"); // unscaled value = 314, scale = 3
BigDecimal b = new BigDecimal("3.140"); // unsclaed value = 314, scale =4
// 주솟값을 비교한다
// false
a == b;
// unscaled value와 scale을 비교한다 (값과 소수점 자리까지 함께 비교)
// false
a.equals(b);
// unscaled value만 비교한다 (값만 비교)
// true
a.compareTo(b) == 0;Kotlin
val a = BigDecimal("3.14")
val b = BigDecimal("3.140")
// equalsTo()와 동일
// false
a == b
// compareTo()와 동일
// true
a >= b
// true
a.compareTo(b) == 0
3) 소수점 처리
BigDecimal의 올림, 내림 등 소수점 처리를 위해서는 RoundingMode가 사용됩니다. RoundingMode는 java.math 패키지에 정의된 Enum 클래스로 다양한 소수점 처리 전략을 제공하고 있습니다. Enum의 value에는 BigDecimal의 상수가 담기게 되는데, 상수를 직접 참조하는 방식은 Java 9부터 Deprecated 되었으므로 RoundingMode를 사용해야 합니다.
package java.math;
public enum RoundingMode {
// 0에서 멀어지는 방향으로 올림
// 양수인 경우엔 올림, 음수인 경우엔 내림
UP(BigDecimal.ROUND_UP),
// 0과 가까운 방향으로 내림
// 양수인 경우엔 내림, 음수인 경우엔 올림
DOWN(BigDecimal.ROUND_DOWN),
// 양의 무한대를 향해서 올림 (올림)
CEILING(BigDecimal.ROUND_CEILING),
// 음의 무한대를 향해서 내림 (내림)
FLOOR(BigDecimal.ROUND_FLOOR),
// 반올림 (사사오입)
// 5 이상이면 올림, 5 미만이면 내림
HALF_UP(BigDecimal.ROUND_HALF_UP),
// 반올림 (오사육입)
// 6 이상이면 올림, 6 미만이면 내림
HALF_DOWN(BigDecimal.ROUND_HALF_DOWN),
// 반올림 (오사오입, Bankers Rounding)
// 5 초과면 올리고 5 미만이면 내림, 5일 경우 앞자리 숫자가 짝수면 버리고 홀수면 올림하여 짝수로 만듦
HALF_EVEN(BigDecimal.ROUND_HALF_EVEN),
// 소수점 처리를 하지 않음
// 연산의 결과가 소수라면 ArithmeticException이 발생함
UNNECESSARY(BigDecimal.ROUND_UNNECESSARY);
...
}
RoundingMode는 다음과 같이 사용할 수 있습니다. setScale()의 첫 번째 인자로 scale(소수점 오른쪽의 자릿수)을, 두 번째 인자로 RoundingMode를 넘겨줍니다. 만약 RoundingMode를 지정하지 않는다면 기본 전략으로 UNNECESSARY가 적용됩니다.
// 0.2
new BigDecimal("0.12345").setScale(1, RoundingMode.UP);
// -0.2
new BigDecimal("-0.12345").setScale(1, RoundingMode.UP);
// 0.1
new BigDecimal("0.12345").setScale(1, RoundingMode.DOWN);
// -0.1
new BigDecimal("-0.12345").setScale(1, RoundingMode.DOWN);
// 0.2
new BigDecimal("0.12345").setScale(1, RoundingMode.CEILING);
// -0.1
new BigDecimal("-0.12345").setScale(1, RoundingMode.CEILING);
// 0.1
new BigDecimal("0.12345").setScale(1, RoundingMode.FLOOR);
// -0.2
new BigDecimal("-0.12345").setScale(1, RoundingMode.FLOOR);
// 1
new BigDecimal("0.5").setScale(0, RoundingMode.HALF_UP);
// 0
new BigDecimal("0.5").setScale(0, RoundingMode.HALF_DOWN);
// 0
new BigDecimal("0.5").setScale(0, RoundingMode.HALF_EVEN);
// 2
new BigDecimal("1.5").setScale(0, RoundingMode.HALF_EVEN);
// java.lang.ArithmeticException: Rounding necessary
new BigDecimal("0.12345").setScale(1, RoundingMode.UNNECESSARY);
// java.lang.ArithmeticException: Rounding necessary
// RoundingMode.UNNECESSARY가 적용됨
new BigDecimal("0.12345").setScale(1);
// 0.0
new BigDecimal("0.00000").setScale(1);
// 0.12345
// 맨끝의 0을 절사
new BigDecimal("0.12345000").stripTrailingZeros();
소수점 처리에는 MathContext를 사용할 수도 있습니다. MathContext은 정밀도(precision)와 RoundingMode를 하나로 묶은 클래스입니다.
public final class MathContext implements Serializable {
public static final MathContext UNLIMITED =
new MathContext(0, RoundingMode.HALF_UP);
public static final MathContext DECIMAL32 =
new MathContext(7, RoundingMode.HALF_EVEN);
public static final MathContext DECIMAL64 =
new MathContext(16, RoundingMode.HALF_EVEN);
public static final MathContext DECIMAL128 =
new MathContext(34, RoundingMode.HALF_EVEN);
...BigDecimal a = new BigDecimal("7");
BigDecimal b = new BigDecimal("3");
// 전체 자릿수를 제한하지 않음
// java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
a.divide(b, MathContext.UNLIMITED);
// 전체 자릿수를 7개로 제한하고 HALF_EVEN을 적용
// 2.333333
a.divide(b, MathContext.DECIMAL32);
// 전체 자릿수를 16개로 제한하고 HALF_EVEN을 적용
// 2.333333333333333
a.divide(b, MathContext.DECIMAL64);
// 전체 자릿수를 34개로 제한하고 HALF_EVEN을 적용
// 2.333333333333333333333333333333333
a.divide(b, MathContext.DECIMAL128);
BigDecimal 사용 시 주의할 점
마지막으로 BigDecimal을 사용 시 주의할 점을 다시 한번 정리하면서 글을 마치도록 하겠습니다.
1) double 생성자 대신 String 생성자를 사용하여 BigDecimal 생성하기
double은 근삿값을 담고 있기 때문에 이를 사용하여 BigDecimal을 생성하면 정확한 값이 들어가지 않습니다. 따라서 String 생성자나 valueOf() 메서드를 사용해서 BigDecimal을 생성해야 합니다.
new BigDecimal(1.12); // 1.12000000000000010658141036401502788066864013671875
new BigDecimal("1.12"); // 1.12
BigDecimal.valueOf(1.12); // 1.122) 소수점 처리 전략을 설정할 것
소수점 처리를 하지 않으면 특정 연산 시 ArithmeticException이 발생할 수 있습니다. 따라서 적절한 소수점 처리 전략을 수립하는 것이 중요합니다.
// 나누기 - 기본적으로 정확한 몫을 반환함
// 2.33333...
// java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
a.divide(b);
// 나누기 - 총 자릿수를 제한하지 않고 반올림
// 2.33333...
// java.lang.ArithmeticException: Non-terminating decimal expansion; no exact
a.divide(b, MathContext.UNLIMITED);
// java.lang.ArithmeticException: Rounding necessary
// RoundingMode.UNNECESSARY가 적용됨
new BigDecimal("0.12345").setScale(1);Kotlin을 사용중이라면 확장 함수를 이용해서 프로젝트 내의 특정 연산에 대한 소수점 처리를 공통적으로 수행할 수 있습니다.
// https://jsonobject.tistory.com/466
operator fun BigDecimal.div(other: BigDecimal): BigDecimal = this.divide(other, BigDecimalUtils.SCALE_SIX, BigDecimalUtils.BANKERS_ROUNDING_MODE)
class BigDecimalUtils {
companion object {
const val SCALE_SIX = 6
val BANKERS_ROUNDING_MODE = RoundingMode.HALF_EVEN
}
}
3) 동등성 비교 시 compareTo()와 equals() 사용을 구분하기
equals()는 unscaled value과 scale을 모두 비교하는 반면, compareTo()는 unscaled value만을 비교합니다. 즉, equals()는 값과 소수점 이하의 자릿수를 모두 비교하고 compareTo()는 값만 비교한다고 할 수 있습니다. 이에 유의하여 적절한 함수를 사용해야 합니다.
특히 API 통신 시엔 별도의 deserializer 설정이 없다면 JSON 역직렬화 과정에서 의도치 않은 값이 할당될 수 있으므로 역직렬화된 객체의 BigDecimal 필드를 비교할 땐 더욱 주의해야 합니다. 사실 대부분의 상황에선 값만을 비교할 뿐, 소수점 이하의 자릿수까지 체크해야 하는 경우는 거의 없으므로 헷갈린다면 compareTo() 사용을 추천드립니다.
JSON
{
"price": 0
}Java
BigDecimal price = fetchAPI().getPrice(); // BigDecimal("0.0000")
response.price.equalsTo(BigDecimal.ZERO) // false
response.price.compareTo(BigDecimal.ZERO) == 0 // trueKotlin
val price: BigDecimal = fetchAPI().price // BigDecimal("0.0000")
response.price == BigDecimal.ZERO // false
response.price.compareTo(BigDecimal.ZERO) == 0 // true
3. 참고
'Backend' 카테고리의 다른 글
| 달리는 인증 서비스의 NoSQL을 바꾸자. - 전략편 (0) | 2023.05.03 |
|---|---|
| Testcontainers로 통합테스트 만들기 (0) | 2023.04.26 |
| docker-compose를 이용하여 로컬 개발환경 구성하기(Part1) (2) | 2023.04.12 |
| 초보 개발자를 위한 Redis Cluster Migration 가이드라인 (1) | 2023.03.28 |
| Redis Lua Script를 이용해서 API Rate Limiter개발 (4) | 2023.03.16 |
